Aの2乗をA=(a+b)の2乗と考える力の話
◯に同じ数字が入るとして、
「◯×◯の掛け算」を覚えたことがある人も多いはず
2×2=4
3×3=9
4×4=16
・
・
・
9×9=81
という風に、同じ数をかける掛け算をやっていくと、
10×10=100
というところまでは、義務教育の中で当たり前のように身につけるはずです。
そこから先、「11×11=121」「12×12=144」・・という風に、10を超えた2桁同士の掛け算を覚えた人は、どのくらいいるでしょうか?
受験勉強をやってきた人であれば、10の位の掛け算(「19×19=361」まで)は覚えるのが当たり前という基準があるはずです。
僕は中学受験をする時(小6くらいかな?)に覚えてしまい、改めて中学生の数学の授業で丸っと覚えて、大学受験まで普通に反射的に用いていました。
21×21をどう考えるか?
そこから少し話を発展させます。
「20×20=400」というのは当たり前にわかりますよね。
じゃあ、「21×21」の計算をどうしますか?
覚えている人は441とその場で答えが出る人もいるはずですが、そうじゃない人はどう計算しますか?筆算を書きますか?
僕は反射的に答えがすぐ出てくるのですが、一歩立ち止まって考えてみると実は、
21×21
=(20+1)×(20+1)
=(20+1)^2(※2乗という意味)
と分解をして考えているわけです。これは無意識的にやっています。
おそらく大学で理系の人もしくは高校で理系コースを選んだ人は「ああ、なるほど」と思ってもらえるはずです。
これは実は中学数学で習う「展開」の公式を用いています。
A = (a+b)の2乗
= a^2 + 2ab + b^2
というアレです。わかりやすい画像を貼ると、これの1番です。
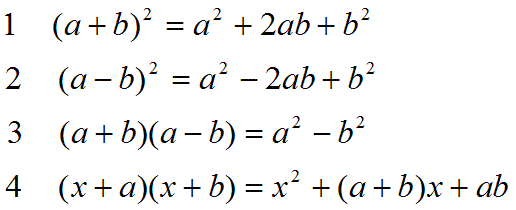
懐かしいですね。笑
見たことある人も多いはず。というか義務教育で習うので絶対知ってるはず・・・
話を戻して、「21×21」の計算の続きです。
21×21
=(20+1)×(20+1)
=(20+1)^2(※2乗という意味)
= 20^2 + 2×20×1 + 1^2
= 400 + 40 +1
= 441
これが答えで、僕の頭の中で瞬間的に行われていることです。
1秒で答えが出ます。
数学で学ぶ「分解」と「応用」は絶対に社会に出て役に立つ
もうちょっとだけ、数学の話をさせて下さい。
先ほど上で使ったのは「展開公式」というものですが、その逆を「因数分解」と言います。
おっと、聞いたことがあるって?笑
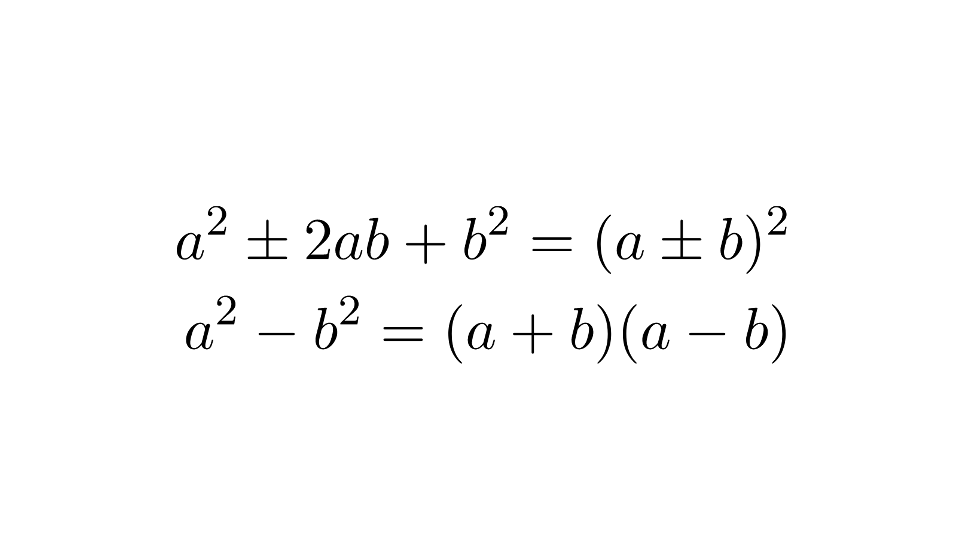
これですね。上で書いた「展開公式」の左右を入れ替えた形になっています。
数学で身につける力は色々ありますが、その中に1つに「まとめる力」というものがあります。
因数分解を習ったときに「共通項でまとめる」という表現を聞いたことがある人もいるはずです。(というか、絶対に聞いていますよ中学で習うのですから笑)

こういうやつですね。
で、この「共通因数でくくる」という考え方は、ものすご〜く社会に出て生きてきます。
例えば、あなたが営業マンだとする。
製品Aは売れるけれど、製品Bは売れない。
でも、製品Cは売れる。なぜだろう?と。
このとき「製品AとCの共通項を見出す」という考え方こそが「因数分解」という考え方なのです。
その共通項とは、例えば、
・◯◯のような顧客に売れる
・ーーの時期にときに決まって売れる
・こういう営業マンだと売れる
・製品Dとセットだと売れやすい
etc..
こういうことを考える「考え方の脳みそ」を築き上げるのが、数学を学ぶ大きな意味だと思うのです。
一方で、その「分解したもの」を広げるのが「展開」という考え方です。
(数学的にいうと、項の和にする、と言います)
一番最初に書いた「21×21=441」というのは「展開公式」を用いて考えました。
この「展開」という考え方は、要は応用ですね。
広げる公式を、応用していくという考え方も言わずもがな、社会に出て本当に役に立ちます。
(例を書くとうるさくなるので割愛しますが・・)
数学は役に立つのか?という議論をすると必ず「サインコサインなんて、社会に出て使ったことがない!」だとか「微分・積分なんて、どこで使うんだ?」という議論になります。
でも、それらをちゃんと原理原則から学んだ僕から言わせてもらいます。
オブラートに包んで表現すると「社会に出てこんなに高等数学が役に立つとは思っていなかった」と思っています。
本当の話。
サインコサインというのは三角関数のことです。
微分・積分とは「傾き(相関係数の可視化)」とか「面積の計算(売上の最大化)」という考え方で絶対に使います。
というか、それを知らないでビジネスを考えられると思っていること自体が意味不明です。
そのくらい役に立ちます。
オブラートに包んで書いていますが、まだまだたくさんあります。
そういうことはこの「現象を物理学で捉える」というカテゴリで書いていこうと思っているので、少しずつ書き溜めていきますね。
時々遊びに来てくれたら嬉しいです。
今日も読んでくださって、ありがとう。
<追伸>
ついでと言っては何ですが、オブラートに包まずに表現すると「微分・積分すらわからないバカと会話をするのは疲れるから、話をしたくない」というのが本音です。ごめんね・・
<追伸の追伸>
何も「偏微分方程式を解け」とか「シュレディンガー方程式を解け」と言っているわけではないのです。
センター試験レベルまででも良いので、きちんと数学を学びなおすと、見える景色が一変すると思うのですが、いかがでしょうか。
<追伸×3>
そういえばこの前、社会人になって初めて「医学部受験生の家庭教師をしてほしい」と頼まれました。
聞いてみると、とある御曹司で、20歳を過ぎてもなお浪人をしているそう。
「お金はすごく払うから」と言われましたが、、











